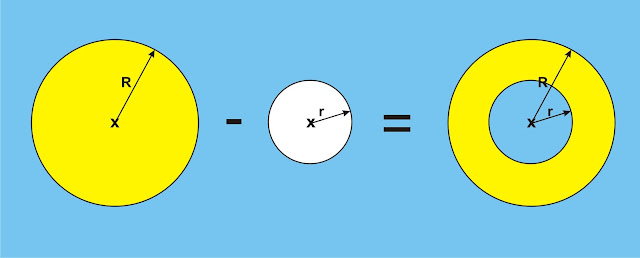SOLUCIONES A LOS EJERCICIOS DEL 26 DE MARZO DE 2013

1. F = 199 + 1.30 A
2. $ 3,500
3. M = log (Am / Ac)
4. A = (2Y)(Y) que también puede escribirse así: A = 2Y²
5. a α F / m
6. π ( R² - r² ) = A

7. F α (Q₁)(Q₂) /r²
8. F' = (1/9) F
9. F' = 16F
10. F' α (2/3)F
11. A = 2X² + 9X + 9
12. X + 1/3 X + 2/3 X + 4/3 X = 300

Si deseas ver algún posible desarrollo de las soluciones:

1. Cierta compañía telefónica ofrece un plan de renta mensual (R) por $199 que incluyen 40 minutos libres y $1.30 por cada minuto adicional (A) ¿Cuál es el modelo matemático que permite calcular el valor de la factura (F) mensual?

Valor de factura =  Renta   +   Costo total de minutos adicionales
        F               =     R       +         1.30 por cada minuto (A)
        F               =     199    +          1.30 (A)
        
F =  199 + 1.30 A
_________________________________________________________________________

2. Se recubrirá el piso de un baño que mide 1.8 X 3 m utilizando azulejos de 20 X 20 cm y la caja de azulejo contiene 10 piezas ¿cuál será el costo total si la caja cerrada se vende en 250 pesos?

Los mosaicos son cuadrados y ajustan con enteros a lo largo y ancho del baño; es decir, no sobran ni falta espacio por cubrir, como se muestra en la figura:

Se necesitan 15 mosaicos a lo largo y  9 mosaicos a lo ancho:
entonces: 15 X 9 = 135 mosaicos.

Si se compran 13 cajas, se tendrían 13 X 10 = 130 mosaicos y faltarían 5
La caja se vende cerrada, entonces es necesario comprar: 14 cajas
La solución es: 14 cajas por $ 250 = $ 3,500  

Otra alternativa para calcular el número de mosaicos:

Se calcula el área del baño, pero en centímetros cuadrados:
3 m = 300 cm    y     1.8 m = 180 cm
300 cm X 180 cm = 54, 000 cm cuadrados.

Ahora se calcula el área de un sólo mosaico:
20 cm X 20 cm = 400 cm cuadrado

Y se divide: 54,000 / 400 = 135 mosaicos,
La solución es: 14 cajas por $ 250 = $ 3,500
_________________________________________________________________________

3. Richter definió la magnitud (M) de un terremoto, en función de la energía liberada. Así, la magnitud (M) es el resultado de obtener el logaritmo (log) del cociente de la Amplitud Máxima (Am) entre la Amplitud Corregida (Ac) ¿Qué modelo matemático expresa la situación planteada?

La Magnitud = Logaritmo del cociente de (la amplitud máxima (Am) entre la amplitud corregida (Ac))

        M         =        Logaritmo    ( Am entre Ac)

        M        =         Logaritmo ( Am / Ac)

        M = log (Am / Ac)
_____________________________________________________________________

4. Se busca determinar el área (A) de un terreno cuya largo es el doble el ancho ¿cuál es el modelo matemático que representa la situación planteada en función del ancho (Y).

El área de un rectángulo es igual a la base multiplicada por la altura:

Área (A)   igual a      la base      por     la altura
A             =        ( base )       POR      ( altura );

Me dicen que la altura es el ancho y que le ponga la letra "Y":
A             =        ( base )       POR      ( Y );

además, la base mide el doble del ancho....... base = 2Y
A             =        (2Y )       POR      ( Y );

Finalmente:

A = (2Y)(Y)
que también puede escribirse:
A = 2Y²
____________________________________________________________________

5. En 1687 Newton publicó Philosophiae Naturalis Principia Mathematica, donde estableció los principios de la mecánica teórica. Tres de estos principios son las tres leyes que llevan el nombre de este científico inglés. La segunda ley establece: "...la aceleración es directamente proporcional a la fuerza resultante que se aplica a un cuerpo, e inversamente proporcional a la masa del mismo." ¿Cuál es la expresión matemática que se desprende de este principio físico?

La proporcionalidad directa entre dos variable, por ejemplo A y B, se expresa

A α B

La proporcionalidad inversa entre dos variable, por ejemplo A y C, se expresa:

A α 1 / C

Juntando las dos expresiones:
A α  B / C, que se lee: " A es directamente proporcional a B e inversamente proporcional a C.

Así, la Segunda Ley de Newton:  "...la aceleración (a) es directamente proporcional a la fuerza resultante (F) que se aplica a un cuerpo, e inversamente proporcional a la masa (m) del mismo." se expresa:

a α  F / m

_________________________________________________________________________

6. Una fábrica de roldanas quiere establecer la fórmula que permite calcular el área del material utilizado en la elaboración de roldanas de diferentes dimensiones, considerando que el radio de la circunferencia externa es "R" y el radio de la circunferencia interna es "r" ¿Cuál sería dicha fórmula?

Hagamos un gráfico para ver que la roldana se obtiene:

Tomando el círculo mayor y restando el círculo menor.
(Nota: El área de un círculo es Pi por radio cuadrado)

Calculando áreas:
            Área mayor                           -             área menor                               =   Área de la roldana
Pi por radio mayor (R) cuadrado       -             Pi por área menor(r) cuadrado  =   Área Roldana (A)

Pi por R cuadrado                             -             Pi por r cuadrado                      =  Área Roldana (A)
Pi por R²                              -           Pi por r^{2                               = A}
πR²                                       -           πr^{2                                           = A}
πR²  -   πr²   =   A  Observa que π se multiplica en ambos términos

π multiplica a R² y a - r²
π por R²  y a -r² = A
π ( R²  - r² ) = A

π ( R²  - r² ) = A

_____________________________________________________

7. Charles-Augustin de Coulomb fue un físico francés del siglo 18 quien en 1785 estableció la función que lleva su nombre: "Ley de Coulom". Este principio expresa que: "..la magnitud de la fuerza (F) ejercida por cargas (Q1 y Q2) es directamente proporcional al producto de su cargas e inversamente proporcional al cuadrado de la distancia (r) que las separa". Indica el modelo matemático de este enunciado.

"..la magnitud de la fuerza (F) ejercida por cargas (Q1 y Q2) es directamente proporcional al producto de su cargas..."

La fuerza (F)  directamente proporcional al producto de las cargas (Q₁ y Q₂)
F α  producto de Q₁ por Q₂     Producto significa multiplicación:
F α  (Q₁ por Q₂)
F α  (Q₁)(Q₂), dejémoslo aquí, por un momento, veamos la segunda parte del enunciado.

"...e inversamente proporcional al cuadrado de la distancia (r) que las separa"

F α  1/distancia (r) cuadrada. La proporción inversa se vio en el problema número 5

F α  1/(r) cuadrada

F α  1/r²

Uniendo F α  (Q₁)(Q₂)  con  F α  1/r²

F α  (Q₁)(Q₂)/r^{2
_________________________________________________________}

8. A partir del enunciado del problema anterior, ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F) si la distancia (r) entre las dos cargas (Q1 y Q2) se triplicara?

Una proporción inversa entre dos variables significa que cuando una variable aumenta, la otra variable disminuye.
Observa que en la ley que Coulomb, la distancia va cuadrada, entonces:
Si aumenta la distancia, la fuerza disminuye en relación al cuadrado.
Si la distancia aumenta 5 veces, la fuerza disminuye  5²; es decir disminuye 25 veces (1/25 del original)
Si la distancia aumenta 4 veces, la fuerza disminuye 4² ; es decir, disminuye 16 veces (1/16 del origina)

Si la distancia se triplica, es decir aumenta 3 veces, la fuerza disminuye 3²; es decir, disminuye 9 veces (1/9 del original):

La nueva fuerza (F') será la novena parte de la fuerza original (F)
    F' = novena parte de (F)

    F' = (1/9) F
_________________________________________________________________________

9. Si en lugar de triplicarse. la distancia (r) se redujera a la cuarta parte, ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F)

Por el contrario del problema anterior, si la distancia disminuye, la fuerza aumenta en relación al cuadrado.
Si la distancia se reduce a 1/10 de la original, la fuerza aumenta 10²; es decir aumenta 100 veces.
Si la distancia se reduce a 1/9 de la original, la fuerza aumenta 9²; es decir, aumenta 81 veces
Si la distancia se reduce a 1/6 de la original, la fuerza aumenta 6²; es decir, aumenta 36 veces
Si la distancia se reduce a 1/5 de la original, la fuerza aumenta 5²; es decir, aumenta 25 veces

Si la distancia se reduce a 1/4 de la original, la fuerza aumenta 4² de la fuerza (F) original; es decir, aumenta 16 veces

F' = 16F
__________________________________________________________________________

10. Supongamos ahora que la distancia no varía, pero una de las cargas aumenta al doble y la otra se reduce a la tercera parte ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F)

De manera más formal:

F α  (Q1)(Q2)

F' α  (Q'1)(Q'2)   como Q'1=2Q1    y Q'2=1/3Q'2

F' α  (2Q1)(1/3Q2)

F' α  (2)(1/3)(Q'1)(Q'2)

F' α  (2/3)(Q'1)(Q'2)

Pero recuerda que F α  (Q1)(Q2)

F' α  (2/3)F

La nueva fuerza será 2/3 de la fuerza anterior.
________________________________________________________________________


11. Se tiene un terreno rectangular cuya longitud es el doble que el ancho. Si a este terreno se le agregara tres metros de cada lado ¿qué expresión permitiría calcular el área?

Observa que se tienen tres rectángulos y un cuadrado: Uno grande de color morado de  2X por X; Dos amarillos, uno de 3 por 2X y otro de 3 por X; y un cuadrado verde, de 3 por 3.

Te recuerdo que las áreas de cada cuadrilátero se calculan multiplicando lado por lado:
Morado:  (2x) por (x).................................... 2X²
Amarillos: (3)(X)  y (2X) por (3)................... 3X y 6X
Verde: (3)(3)................................................ 9

Área total = área morada +  áreas amarillas +  área verde
A         =             2X²          +     3X + 6X    +         9

Podemos reducir las áreas amarilla: 3X + 6X= 9X



A         =             2X²          +     9X      +         9

A  =   2X²   +   9X    +     9

(Nota: Pregunta a tu profesor sobra la multiplicación de dos binomios y replantea la solución)
_______________________________________________________________________________

12. Durante cuatro días se obtiene el siguiente registro de asistencia del  público: El primer día asistió cierta cantidad; el segundo día, sólo tuvo la tercera parte que el primer día; el tercer día registro el doble que el segundo día; y, el cuarto día, el doble que el tercer día. La suma total de audiencia fue de 300 personas. ¿Qué modelo matemático permite representar la situación planteada?

"primer día" "cierta"................................................."cierta" = X                            X       .... 1° día
"segundo día" "tercera parte que primer día"..............(1/3)(1° día)                       1/3 X    .... 2° día
"tercer día" "el doble que el segundo día" .................... Doble que 2° día             2(1/3 X)   ....3°  día
el cuarto día, el doble que el tercer día ....................... Doble que 3° día             2(3° día )
                                                                                                                          2(2(1/3 X)) .. 4° día
La suma total de audiencia fue de 300 personas.
Se suma todo: X +  1/3 X + 2(1/3 X) + 2(2(1/3 X)) = 300 personas
Finalmente:

 X + 1/3 X + 2/3 X + 4/3 X = 300

*************************************************************

Suscríbete gratis, estos post pueden ayudarte.

Saludos.

Prof. Jorge Mondragón A.
Euzkaro 174-B Col. Industrial
Esq. Fundidora de Monterrey
Del. Gustavo A Madero
México, D.F
Móvil: 553 949 6921
No respondo SMS, en todo caso usar:
Viber, WhatsApp
Mail: ceneval_sep@hotmail.com, 286ceneval@gmail.com



CURSOS Y GUÍAS:
Visita el blog: http://ceneval286.blogspot.com

EJERCICIOS DE COMPRENSIÓN DE LECTURA:
Visita mi blog: http://comprension-de-lecturas.blogspot.mx/

RESULTADOS DEL EXAMEN DE ENERO DE 2013
Visita mi blog: http://ceneval286.blogspot.mx/2013/03/resultados-ceneval-enero-2013.html

EJERCICIOS DE LENGUAJE MATEMÁTICO. CAMPO DE COMPETENCIA: MATEMÁTICAS. EXAMEN CENEVAL MAYO 2013

EJERCICIOS DE LENGUAJE MATEMÁTICO.

Examen del Ceneval, Acuerdo 286, mayo de 2013

1. Cierta compañía telefónica ofrece un plan de renta mensual (R) por $199 que incluyen 40 minutos libres y $1.30 por cada minuto adicional (A) ¿Cuál es el modelo matemático que permite calcular el valor de la factura (F) mensual?

2. Se recubrirá el piso de un baño que mide 1.8 X 3 m utilizando azulejos de 20 X 20 cm y la caja de azulejo contiene 10 piezas ¿cuál será el costo total si la caja cerrada se vende en 250 pesos?

3. Richter definió la magnitud (M) de un terremoto, en función de la energía liberada. Así, la magnitud (M) es el resultado de obtener el logaritmo (log) del cociente de la Amplitud Máxima (Am) entre la Amplitud Corregida (Ac) ¿Qué modelo matemático expresa la situación planteada?

4. Se busca determinar el área (A) de un terreno cuya largo es el doble el ancho ¿cuál es el modelo matemático que representa la situación planteada en función del ancho (Y).

5. En 1687 Newton publicó Philosophiae Naturalis Principia Mathematica, donde estableció los principios de la mecánica teórica. Tres de estos principios son las tres leyes que llevan el nombre de este científico inglés. La segunda ley establece: "...la aceleración es directamente proporcional a la fuerza resultante que se aplica a un cuerpo, e inversamente proporcional a la masa del mismo." ¿Cuál es la expresión matemática que se desprende de este principio físico?

6. Una fábrica de roldanas quiere establecer la fórmula que permite calcular el área del material utilizado en la elaboración de roldanas de diferentes dimensiones, considerando que el radio de la circunferencia externa es "R" y el radio de la circunferencia interna es "r" ¿Cuál sería dicha fórmula?

7. Charles-Augustin de Coulomb fue un físico francés del siglo 18 quien en 1785 estableció la función que lleva su nombre: "Ley de Coulom". Este principio expresa que: "..la magnitud de la fuerza (F) ejercida por cargas (Q1 y Q2) es directamente proporcional al producto de su cargas y inversamente proporcional al cuadrado de la distancia (r) que las separa". Indica el modelo matemático de este enunciado.

8. A partir del enunciado del problema anterior, ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F) si la distancia (r) entre las dos cargas (Q1 y Q2) se triplicara?

9. Si en lugar de triplicarse. la distancia (r) se redujera a la cuarta parte, ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F)

10. Supongamos ahora que la distancia no varía, pero una de las cargas aumenta al doble y la otra se reduce a la tercera parte ¿cuál sería la nueva magnitud de la fuerza (F') con respecto de la fuerza anterior (F)

11. Se tiene un terreno rectangular cuya longitud es el doble que el ancho. Si a este terreno se le agregara tres metros de cada lado ¿qué expresión permitiría calcular el área?

12. Durante cuatro días se obtiene el siguiente registro de asistencia del  público: El primer día asistió cierta cantidad; el segundo día, sólo tuvo la tercera parte que el primer día; el tercer día registro el doble que el segundo día; y, el cuarto día, el doble que el tercer día. La suma total de audiencia fue de 300 personas. ¿Qué modelo matemático permite representar la situación planteada?

Las soluciones vendrán en el siguiente post.

Suscríbete gratis, estos post pueden ayudarte.

Saludos.

Prof. Jorge Mondragón A.
Euzkaro 174-B Col. Industrial
Esq. Fundidora de Monterrey
Del. Gustavo A Madero
México, D.F
Móvil: 553 949 6921
No respondo SMS, en todo caso usar:
Viber, WhatsApp
Mail: ceneval_sep@hotmail.com, 286ceneval@gmail.com



CURSOS Y GUÍAS:
Visita el blog: http://ceneval286.blogspot.com

EJERCICIOS DE COMPRENSIÓN DE LECTURA:
Visita mi blog: http://comprension-de-lecturas.blogspot.mx/

RESULTADOS DEL EXAMEN DE ENERO DE 2013
Visita mi blog: http://ceneval286.blogspot.mx/2013/03/resultados-ceneval-enero-2013.html

REDUCCIÓN DE NÚMEROS POSITIVOS Y NEGATIVOS.

Ejercicio 1

Reduce las siguientes operaciones, yo resuelvo algunos:
8 + 3 = 11 Suman 11 y anotamos el signo del 8, porque es el de mayor valor absoluto.
- 5 - 4 = - 9 Suman 9, pero le ponemos signo negativo porque el de mayor valor absoluto es el -5
6 + 7
- 8 - 12
13 + 14
- 15 - 10
5 - 8 = - 3 Se restan porque son de distinto signo, colocamos el signo del -8 porque es el de mayor valor absoluto.
16 - 23
14 - 12
- 15 + 18
- 23 + 24 = +1 Se restan y colocamos el signo del +24 porque es el de mayor valor absoluto
- 46 + 40
- 32 + 30
- 8 + 13
12 - 23
-15 + 19

Un poco más complejos
- 5 + 7 - 8
Primero sumamos por separado negativos y positivos:
+ 7 - 13 los restamos y le ponemos el signo de mayor valor absoluto
+ 7 - 13 = - 6

Es tu turno
6 + 8 - 12
7 - 6 - 4
-8 + 8 + 6
- 9 + 13 + 17
- 8 - 6 + 14

Agreguemos unos números más
-5 + 8 - 7 + 10
Primero sumamos por separado negativos y positivos:
+ 18 - 12 los restamos y le ponemos el signo de mayor valor absoluto
+ 18 - 12 = + 6

- 9 + 4 - 8 + 14
6 - 7 + 8 - 10
- 9 + 16 - 7 + 8
Ahora sin el apoyo de los colores:
- 9 + 10 - 8 + 12 - 4
- 5 + 7 - 9 + 10
4 - 7 + 12 - 9 + 10
12 + 7 - 8 + 10 - 8
6 + 7 - 8 - 4 - 6 + 7 - 8
9 - 7 + 8 - 4 + 7 - 10 + 12 - 15.

Para entregar la siguiente clase.

Atentamente
Prof: Jorge Mondragón
"La educación, camino único hacia el desarrollo"

BIENVENIDOS Y BIENVENIDAS

En este nuevo blog podrán encontrar ejercicios y algunos resúmenes de las clases para el examen del Ceneval. Sien embargo, los problemas que aquí se mostrarán, también pueden servir para preparar otro tipo de exámenes.

Espero que les resulte de utilidad.

Atentamente

"La educación, camino único hacia el desarrollo"

Prof. Jorge Mondragón